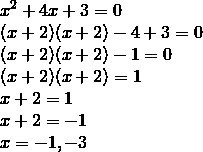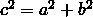東大の先生！文系の私に超わかりやすく数学を教えてください！

これは「中学数学の要点を5〜6時間でさくっと終わらせる」本である
著者によると、数学とは大きく三つの分野に分けられる
- 代数（algebra） = 数・式
- 解析（analysis） = グラフ
- 幾何（geometry） = 図解
そして、各分野において、中高生の間に到達すべきゴールが明確にある、という
- 代数のゴール → 二次方程式
- 解析のゴール → 微分・積分
- 幾何のゴール → ベクトル
さらに、中学数学のゴールは以下である、という
- 代数のゴール → 二次方程式
- 解析のゴール → 二次関数
- 幾何のゴール → ピタゴラスの定理と円周角と相似
二次方程式のまとめ
- 二次方程式は「平方完成」で解く
  - 「同じ数のズレ」の形にして解く
  - どんな二次方程式も平方完成で解ける
二次関数のまとめ
- 方程式と関数の違い
  - 方程式 = 代数の話
    - 特定の条件のときの x の値を求める
    - 点を表現するときに使う
  - 関数 = 解析の話
    - 関係性を示す式そのもの
    - 線を表現するときに使う
幾何のまとめ
- ピタゴラスの定理
- 相似
  - これ！というキーワードがわからなかった
- 円周角の定理
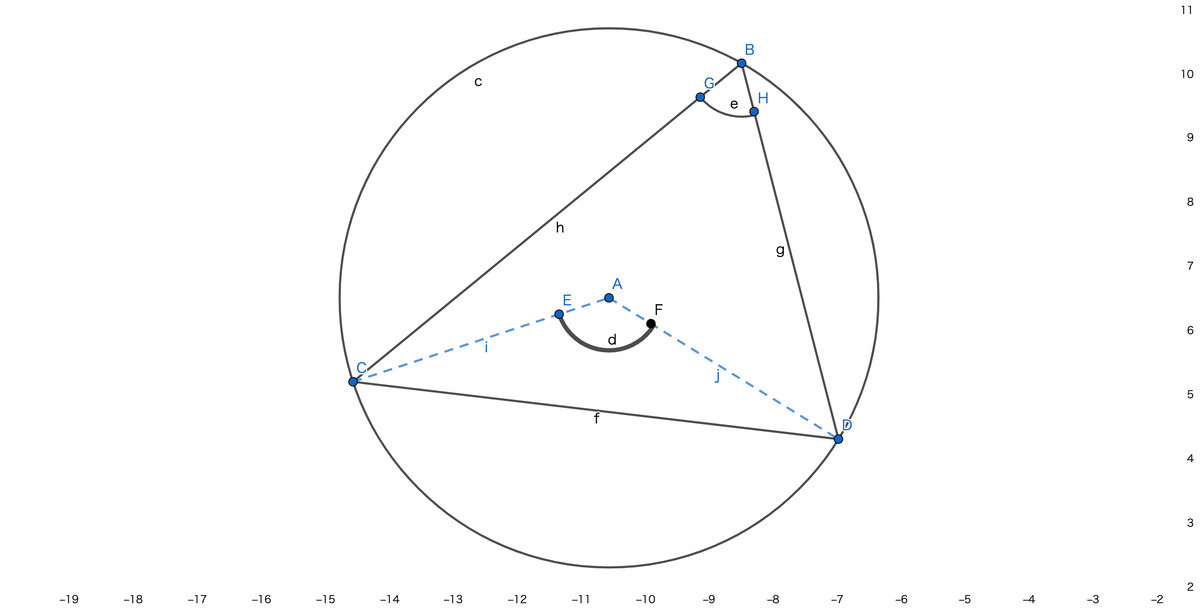
  - 角dは角eの2倍の角度になる
  - Calculator Suite - GeoGebra で作図

「どんな二次方程式も平方完成で解ける」はちょっとした衝撃だった
そもそも「平方完成」という言葉を習った記憶が無い...
この本のハイライトもそのあたりだったような印象
後半は説明が駆け足というか、ちょっと雑になった気がした
- 自分が集中力を失ってついていけなくなったせいかもしれない
- 特に幾何は苦手意識が強かった分野なので余計に
数学の学び直しをするにあたり、長年の数学アレルギーを払拭する取っ掛かりの一つとするには悪くなさそう

思考体力とは
1. 自己駆動力
2. 多段思考力
3. 疑い力
4. 大局力
5. 場合分け力
6. ジャンプ力

多段思考力とは「AならB、BならC、CならD......」と、思考した結果をどんどん積み上げながら、答えが見つかるまで何段も諦めずに考え続ける力のこと。

数学者にとって解析とは基本的に「微分積分を使うこと」なんです。もしビジネスパーソンがデータをたくさん集めて、「こんな傾向があるかな？」みたいに感覚的に推測するだけなら、それは解析ではなく「仮設を立てているだけ」

関数の線は、傾きの集合体

解析という分野は、1つの点の周りにどれだけ他の点が密集して、どういう状態で配置されているかを「解析」するもの

中学では微分積分を習わないので「傾き」という言葉でお茶を濁しているだけ

関数にかけ算が含まれると必ず曲線になる
  - 変数同士のかけ算が含まれると、必ず曲線になる

逆に、かけ算を含まない関数は必ず直線、つまり一次関数になる

@kyanny's blog